RSA нь олон нийтийн түлхүүрт криптографийн хамгийн түгээмэл алгоритм бөгөөд 1977 онд Райвест, Шамир, Адлеман нараар зохиогдсон.

Үндсэн зарчим:

RSA нь хоёр түлхүүр ашигладаг:

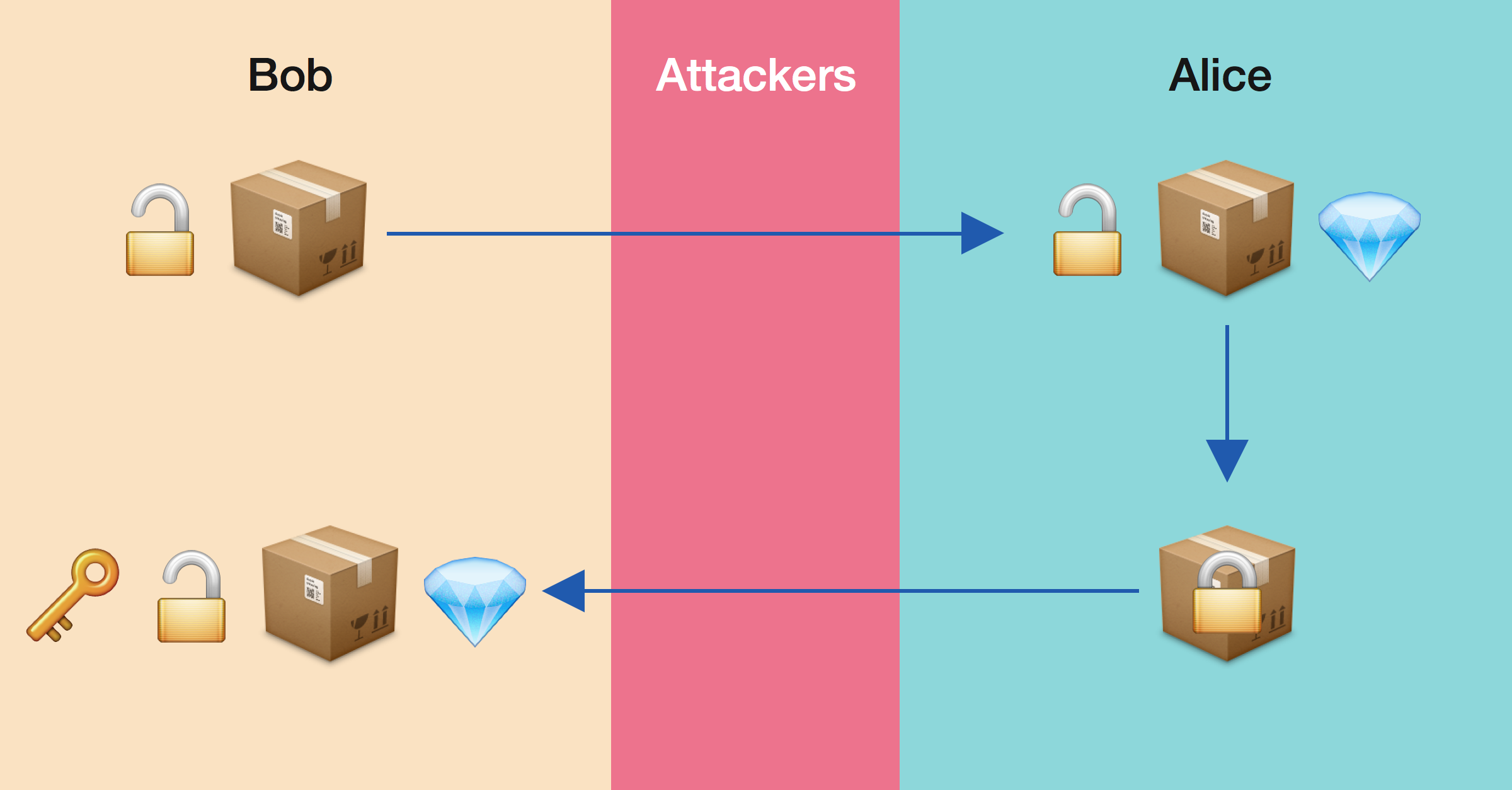
1. Нийтийн түлхүүр – хүн бүрт мэдэгдээд зориулагдсан, мессеж шифрлэхэд хэрэглэгддэг
2. Хувийн түлхүүр – зөвхөн эзэмшигчид мэдэх, шифрлэгдсэн мессежийг тайлах (дешифрлэх) зориулалттай

Хэрхэн ажилладаг вэ?

Шифрлэх үйл явц:

• Хэн нэгэн танд мессеж илгээх гэж байна
• Тэд таны нийтийн түлхүүрийг ашиглан мессежээ шифрлэдэг
• Шифрлэгдсэн мессежийг танд илгээдэг

Тайлах үйл явц:

• Та шифрлэгдсэн мессежийг хүлээн авна
• Зөвхөн таны мэдэх хувийн түлхүүрээр тайлна
• Анхны мессежийг уншина

Математик үндэслэл (хялбаршуулсан):

RSA нь том тоог үржүүлэх нь амархан, харин урвуулах (хүчин зүйлчлэх) нь маш хэцүү гэсэн математик зарчим дээр суурилдаг.

Жишээ нь:

• 709 × 733 = 519,697 (тооцоход хялбар)
• 519,697-ыг ямар хоёр анхны тооны үржвэр болохыг олох (маш хэцүү)

Бодит амьдрал дахь жишээ:

Та онлайн банк руу нэвтрэх гэж байна гэж бодъё:

1. Таны браузер банкны нийтийн түлхүүрийг ашиглан мэдээллээ шифрлэдэг
2. Шифрлэгдсэн мэдээлэл интернэтээр дамждаг
3. Зөвхөн банк л өөрийн хувийн түлхүүрээр тайлж чадна
4. Хэрэв хакер мэдээллийг барьсан ч, хувийн түлхүүргүйгээр уншиж чадахгүй

Хэрэглээ:

• Цахим худалдаа
• Мессэж, имэйл шифрлэлт
• VPN холболт
• Дижитал гарын үсэг

RSA нь интернэтийн аюулгүй байдлын үндэс суурь болдог бөгөөд хангалттай урт түлхүүртэй үед (одоогоор 2048 бит ба түүнээс дээш) практик талаас харахад эвдэх боломжгүй гэж үздэг.

Жишээ алгоритм:

// JavaScript Program for implementation of RSA Algorithm

// Function to compute base^expo mod m using BigInt
function power(base, expo, m) {
    let res = BigInt(1); 
    base = BigInt(base) % BigInt(m); 
    while (expo > 0) {
        if (expo & BigInt(1)) {
            res = (res * base) % BigInt(m);
        }
        base = (base * base) % BigInt(m); 
        expo = Math.floor(Number(expo) / 2);
        expo = BigInt(expo);
    }
    return res;
}

// Function to find modular inverse of e modulo phi(n)
function modInverse(e, phi) {
    e = BigInt(e);
    phi = BigInt(phi);
    for (let d = BigInt(2); d < phi; d++) {
        if ((e * d) % phi === BigInt(1)) {
            return d;
        }
    }
    return -1;
}

// RSA Key Generation
function generateKeys() {
    let p = BigInt(7919);  
    let q = BigInt(1009);

    let n = p * q;
    let phi = (p - BigInt(1)) * (q - BigInt(1));

    // Choose e, where 1 < e < phi(n) and gcd(e, phi(n)) == 1
    let e;
    for (e = BigInt(2); e < phi; e++) {
        if (gcd(e, phi) === BigInt(1))
            break;
    }

    // Compute d such that e * d ≡ 1 (mod phi(n))
    let d = modInverse(e, phi);
    return { e, d, n };
}

function gcd(a, b) {
    while (b !== BigInt(0)) {
        let t = b;
        b = a % b;
        a = t;
    }
    return a;
}

// Encrypt message using public key (e, n)
function encrypt(m, e, n) {
    return power(m, e, n);
}

// Decrypt message using private key (d, n)
function decrypt(c, d, n) {
    return power(c, d, n);
}

// Key Generation
let { e, d, n } = generateKeys();

console.log(`Public Key (e, n): (${e}, ${n})`);
console.log(`Private Key (d, n): (${d}, ${n})`);

// Message
let M = 123;
console.log(`Original Message: ${M}`);

// Encrypt the message
let C = encrypt(M, e, n);
console.log(`Encrypted Message: ${C}`);

// Decrypt the message
let decrypted = decrypt(C, d, n);
console.log(`Decrypted Message: ${decrypted}`);

Үр дүн:

Public Key (e, n): (5, 7990271)
Private Key (d, n): (1596269, 7990271)

Original Message: 123
Encrypted Message: 3332110
Decrypted Message: 123